Il dodecaedro serviva per stabilire la data dell’equinozio e centuriare. L’esperimento

Lo studio della meridiana orizzontale di Euporus del museo archeologico nazionale di Aquileia e del Plinthium sive lacunar scolpito da Skopas e citato nel De Architectura di Vitruvio ci consentono di affrontare, e tentare di svelare, l’arcano che si cela dietro l’utilizzo di uno degli oggetti più intriganti dell’antichità: il dodecaedro romano.

Sul dodecaedro questa Testata ha già sviluppato una prima riflessione (https://www.saturniatellus.com/2019/07/dodecaedro-romano-costui-ipotesi-suggestioni-un-mistero-millenario/) articolando una panoramica sintetica delle interpretazioni, oltre ad aver pubblicato un prezioso approfondimento sulla sacralizzazione degli spazi praticata dai romani (https://www.saturniatellus.com/templum/).

Ora torniamo sul tema alla luce di nuovi e interessanti studi.

Descrizione

Il dodecaedro è un piccolo manufatto cavo delle dimensioni che variano dai 4 agli 11 centimetri, realizzato in bronzo o in pietra (è stato reso noto anche qualche ritrovamento in oro) e formato da dodici facce piatte pentagonali i cui vertici s’incontrano a gruppi di tre. Su ogni faccia è presente un foro circolare con diametri diversi: complessivamente, quindi, dodici fori. Su ogni vertice del manufatto sono presenti palline.

L’oggetto è così definito da Francesco Maurolico (1494-1575): “[…] E li platonici assomigliano quattro solidi regolari a questi quattro elementi [Aria, Acqua, Terra, Fuoco.], et il quinto al Cielo […]. Il Dodecaedro al Cielo perché come il Cielo è più ampio di tutti gli elementi, et abbraccia ogni cosa, così il Dodecaedro è il più grande de cinque solidi chiusi intra una sfera, et può circoscrivere ogn’uno del altri […]”.

Fu proprio Platone (428-348 a.C.) a scoprire i solidi simmetrici e per questo motivo il gruppo prende il suo nome. Esso comprende: l’Ottaedro, l’Icosaedro, l’Esaedro, il Tetraedro, ed il Dodecaedro, che ne fece la base per la sua cosmogonia. “[…] E prima di tutto, che Aria, Acqua, Terra, Fuoco siano corpi, è chiaro ad ognuno. Ma ogni specie di corpo ha anche profondità. Restava una quinta combinazione e Dio se ne giovò per decorare l’Universo”, scrive Platone nel Timeo (XX, 55) associando la quinta combinazione – il Dodecaedro – all’intero Creato o a una sorta di etere che dovrebbe pervaderlo tutto.

A parlare di dodecaedro è anche Keplero nel suo Mysterium Cosmographicum (1597) quando immagina un sistema solare come un complesso nidificato di solidi platonici, in cui i raggi delle sfere concentriche associate determinano le orbite dei sei pianeti allora conosciuti: “[…] La Terra è la sfera che misura tutte le altre. Circoscrivi ad essa un Dodecaedro: la sfera che lo comprende sarà Marte. Circoscrivi a Marte un Tetraedro: la sfera che lo comprende sarà Giove. Circoscrivi a Giove un cubo: la sfera che lo comprende sarà Saturno […]”.

Rinvenimenti

Esemplari di dodecaedri romani sono stati rinvenuti principalmente in Germania e uno di loro fa bella mostra di sé all’interno del castello di Saalburg, località dell’Assia poco distante da Bad Homburg. Un altro molto importante fu ritrovato nel centro storico dell’antica Atuatuca Tongeren. Inoltre, a poca distanza dalla bella basilica di Notre-Dame, nell’interessante museo gallo-romano, edificato su sito di una lussuosa villa romana è conservato un altro esemplare del nostro piccolo oggetto in bronzo.

Finora, nella parte nord-occidentale dell’impero, sono stati trovati circa novanta esemplari. Le circostanze dei ritrovamenti non sono chiare. Si ebbero rinvenimenti negli accampamenti militari (13), nelle tombe (3), nei pressi di un santuario (1), nei tesori (2), nel letto di un fiume (3) etc.

La presenza poi del dodecaedro romano nel tesoro numismatico di Membrey, Saint Parize-le-Châtel, rinvenuto nella tomba di una donna facoltosa nei pressi di una villa rustica, dimostrano che il dodecaedro era un oggetto che difficilmente apparteneva a romani di classe e censo poco elevato.

Misurare il tempo

Prima di addentrarci nelle funzioni specifiche del dodecaedro, dobbiamo fare un passo di lato e focalizzare sulla misurazione del tempo in antico.

Nelle ere più remote l’attenzione alla ciclicità del tempo e ai suoi effetti era altissima: la vita e la morte, le stagioni, le semine e i raccolti erano passaggi imprescindibili e fondanti.

Furono gli astronomi – che, all’epoca, ricoprivano spesso anche la carica di sacerdoti – ad abbozzare i primi tentativi di misura, basandosi principalmente sull’osservazione del cielo, del moto apparente delle stelle, dell’avvicendarsi delle stagioni.

Successivamente, quando anche gli eventi umani divennero punti di riferimento per la misurazione del tempo, iniziarono ad occuparsi di questi studi anche annalisti e cronisti. Pensiamo, ad esempio, al computo degli anni per Olimpiade, introdotto in Grecia, nel periodo ellenistico, da Timeo di Tauromenio (350 a.C. – 260 a.C.), che datava gli avvenimenti prendendo come riferimento cronologico appunto i tempi dei giochi. Nella realtà quotidiana poi, i greci si accontentavano di intercalazioni approssimative e ogni πόλις (polis) adottava un proprio calendario.

Per i romani, il primo calendario è probabilmente databile all’VIII secolo a.C., all’epoca della fondazione dell’Urbe, e contava 10 mesi di 30 o 31 giorni, con l’aggiunta di un intervallo intercalare, forse di origine etrusca, per concordare il computo con il ciclo delle stagioni, e quindi con il Sole.

Il successivo calendario di Numa Pompilio, adottato fino al periodo repubblicano, si basava invece, su 12 mesi: 7 di 29 giorni, 4 di 31 e 1 di 28. Il calendario era sincronizzato con il sole attraverso intercalazioni.

Un altro metodo adottato dopo la fine dell’epoca repubblicana e conosciuto con la formula ab Urbe condita, consisteva, invece, nel contare gli anni partendo dalla fondazione di Roma.

Come è noto, la “sistematizzazione definitiva del tempo in Occidente” avvenne con Giulio Cesare.

Il suo calendario, a cui ha dato il nome, Giuliano, è infatti un calendario solare, cioè basato sul ciclo delle stagioni. Fu elaborato dall’ astronomo egizio Sosigene di Alessandria vissuto nel I secolo a.C. e promulgato da Cesare in qualità di pontefice massimo nell’anno 46 a.C.

Per compensare gli errori accumulati in passato e riportare l’equinozio primaverile al 25 marzo, era però necessario introdurre 85 giorni. Allo scopo furono aggiunti due mesi fra novembre e dicembre all’anno precedente, uno di 33 giorni e l’altro di 34; motivo per cui il 46 a.C., durato 445 giorni, fu soprannominato annus confusionis (l’anno della confusione). Questa confusione ebbe varie ripercussioni nei successivi 50 anni fino a circa l’8 a.C. Dopo la morte di Giulio Cesare (44 a.C.) si commisero vari errori facendo diventare bisestili alcuni anni che non lo dovevano essere e saltando quelli corretti. Fu poi Augusto nell’ 8 a.C. a sistemare l’errore, ordinando che per un certo numero di anni non ci fossero più anni bisestili. Il calendario giuliano fu in vigore anche dopo la caduta dell’impero romano di Occidente, rimanendo in uso fino al XVI secolo, quando fu ritoccato dal papa Gregorio XIII.

E’ questo il calendario tutt’ora in vigore in tutto il mondo.

Misurare lo spazio

Premesso quindi che sino a Giulio Cesare ed oltre la certezza delle date non era assicurata da alcun calendario, ma era tuttavia necessaria per effettuare alcune importanti operazioni, torniamo al dodecaedro.

Nel corso degli anni sono state avanzate diverse teorie che hanno tentato di chiarire quale funzione avesse l’oggetto o quale scopo servisse. Queste teorie ipotizzano, nell’ordine, il portacandele, il dado, la testa di scettro, il dispositivo di misurazione geometrica – per limitarci alle più note.

Una spiegazione ufficiale pienamente soddisfacente per anni però è mancata.

Solo in due recenti pubblicazioni di Robert Nouwen (1993) e B.H. Greiner (1995) è stato finalmente fornito un quadro scientifico ed esaustivo di tutti i dati noti riguardanti i dodecaedri romani, insieme ad una confutazione di tutte le precedenti fantasiose teorie basate su analisi poco accurate.

Secondo questi studi, l’intrigante oggettino traforato era il prezioso strumento di lavoro degli agrimensori romani (figure che riunivano le competenze di architetti, geometri e ingegneri) che venne usato sin dal 232 a.C., anno d’approvazione della Lex Flaminia – prima legge che regolamentasse la distribuzione delle terre sottratte ai nemici (in questo caso l’Ager Gallicus nel Piceno) e la centuriazione –  fino a tutto il I secolo d.C., sino a quando cioè si stabilizzò l’utilizzo del calendario Giuliano.

La sua funzione era quella di stabilire il giorno esatto degli equinozi, sua primaverili sia autunnali, visto che era praticamente impossibile risalirvi con certezza attraverso i vecchi calendari.

Il dodecaedro, dunque, fu l’elaborata ed ingegnosa via d’uscita per stabilire con certezza l’evento primaverile ed autunnale e, di conseguenza, procedere con la centuriazione e successiva assegnazione delle terre conquistate. Operazione quest’ultima, importantissima e fondante per la stabilità dell’assetto dello stato romano sotto il profilo religioso, economico, amministrativo e finanziario.
Ecco come avveniva

Assegnare lo spazio

La centuriatio (centuriazione) consisteva nella suddivisione del terreno in rettangoli regolari, delimitati da strade. Iniziava con un rito sacrificale: i sacerdoti, interpretando i segni cosmici (fatti naturali, studio delle viscere degli animali destinati al sacrificio, osservazione del volo degli uccelli…) stabilivano il punto preciso del terreno, il centro, dal quale occorreva iniziare a tracciare le geometrie. Qui veniva scavato un piccolo pozzo (mundus) sul quale veniva celebrato il sacrificio e diveniva così l’ombelico di questo nuovo territorio annesso a Roma, un luogo sacro, attraverso il quale gli uomini entravano in comunicazione con gli dei. Il sacrificio era preliminare ad ogni centuriazione. Ottenuta la benevolenza divina, entravano in funzione gli agrimensori, o meglio i “gromatici”. Il nome deriva loro dalla groma, cioè lo strumento che veniva utilizzato per effettuare le misurazioni. Esistevano vari modelli di grome, secondo le loro funzioni. La più elaborata è quella di Aquileia. Le più semplici consistevano in un’asticella ai cui capi erano sistemate due ampolle eguali di vetro, riempite per metà d’acqua. L’asticella era sistemata su un palo infisso nel terreno e le ampolle fungevano da bolle di livello. Il dodecaedro era invece il congegno di puntamento attraverso il quale si poteva traguardare la posizione del sole dal momento che gli appezzamenti di terreno venivano normalmente orientati secondo il corso del sole. Tenendo, infatti, come riferimento il mundus, i gromatici stabilivano il punto esatto di levata e di tramonto del sole nel giorno dell’equinozio e, lungo questa linea, tracciavano la strada principale della città o dell’appoderamento, da est a ovest, e la chiamavano decumano.

Insomma, il dodecaedro non era certo l’oggettino decorativo da diporto che qualcuno ha voluto credere.

Tecnica d’utilizzo secondo Waemans

Ad aiutare a “confermare sul campo” questa conclusione è anche uno dei più importanti studi sperimentali sui dodecaedri romani mai realizzato. E’ opera del ricercatore olandese G.M.C. Waemans, che lo ha pubblicato nel suo blog (https://www.romandodecahedron.com) nel 2017. Riporto qui alcuni dei più significativi passaggi e un’immagine.

“ … la mia teoria può essere descritta come segue: il dodecaedro era uno strumento di grandezza astronomica con il quale si può misurare l’angolo della luce solare e quindi determinare con precisione una data specifica in primavera e in autunno (…).  Il funzionamento del dodecaedro come strumento di misurazione si basa infatti sull’angolo del sole nel punto più alto della giornata. In un anno solare, la terra viaggia completamente intorno al sole (365 ¼ giorno). L’angolo della terra opposto al sole cambia durante l’anno in un ritmo sinusale. Il sole raggiunge la posizione più alta intorno al 21 giugno, quando il sole raggiunge il tropico del Cancro (grado di latitudine N 23°,27′) e il punto più basso sarà raggiunto intorno al 22 dicembre, quando il sole raggiunge il tropico del Capricorno. (grado di latitudine Z 23°.27′). Il punto equinoziale primaverile e il punto equinoziale autunnale sono rispettivamente il 21 marzo e il 23 settembre, quando il sole ha raggiunto il livello dell’equatore. L’angolo che la luce del sole fa con la terra è soggetto al grado di latitudine in cui ci si trova.

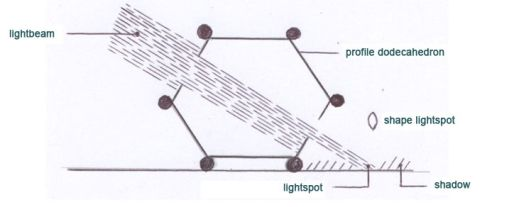
Prendiamo ad esempio la città di Maastricht (Olanda), situata a N 50°.52′. Al 12 marzo e al 23 settembre, l’angolo più grande che la luce del sole forma con la terra a Maastricht è di 90° – 50°,52′ = 39°,08′. Il 21 giugno è 90° – (50°,52′-23°,27′) = 62°,35′ e il 22 dicembre è 90° – (50°,52’+23°,27′ ) = 16°,41′. Quando si è in grado di determinare l’angolo che la luce del sole forma con la terra, si sta effettivamente misurando la data in modo abbastanza accurato.

Secondo le mie ipotesi, l’uso del dodecaedro si basa su queste conoscenze. Si procedeva così: il dodecaedro veniva posto su un piatto orizzontale in una giornata di sole autunnale. Verso mezzogiorno, quando il sole raggiungeva il suo punto più alto di quel giorno, si misurava la luce che cadeva attraverso due aperture opposte. Successivamente, sarebbero stati esaminati venti punti di misurazione per i fasci di luce che attraversavano il foro. Tutto questo andava fatto secondo alcune specifiche. L’ultimo punto di misurazione si otteneva il giorno in cui i raggi del sole passavano attraverso tutti i punti. In primavera si potevano fare le stesse misurazioni.

Per poter poi definire con precisione la data, bisognava calcolare gli angoli dei fasci di luce solare. Anche questi potevano essere misurati con il dodecaedro misurando i due fori opposti. Queste misure sono determinate dal diametro del dodecaedro e dal diametro medio dei due fori opposti l’uno all’altro. L’angolo rettilineo attraverso i due fori opposti è lo stesso per tutti i dodecaedri, cioè 26,6°. Il calcolo presupponeva che il dodecaedro stesse in posizione orizzontalmente. Per ogni dodecaedro si potevano ottenere sei diversi punti di misura (le dodici aree danno sei diverse combinazioni di due fori contrapposti). Con i sei angoli ottenuti si potevano determinare le date corrispondenti. Questi calcoli sono stati fatti con 29 dodecaedri, con i quali per ogni dodecaedro è stata determinata la prima e l’ultima data. I dati necessari, come diametro, misure, fori e il luogo in cui è stato ritrovato, provengono tutti dalla pubblicazione di Nouwen. Il numero di 29 non è stato stabilito a caso. Su questo hanno influito le seguenti considerazioni:

1. Le misurazioni sono utili solo quando si conosce il luogo di ritrovamento del dodecaedro. Senza la data relativa al grado di latitudine, il calcolo non può essere effettuato.
2. Il dodecaedro deve essere in uno stato non danneggiato, in modo che si possa misurare il diametro di tutti i dodici fori.
3. Deve essere nota la posizione attuale del dodecaedro, in modo che gli angoli calcolati possano essere misurati anche per questo campione originale.

I risultati di questi calcoli sono riassunti qui: https://www.romandodecahedron.com/the-hypothesis (…).

Poiché i calcoli mostrano che il periodo di misurazione non supera nella maggior parte dei casi i 30 giorni e sono assenti segni di marcatura sulle aree, ho ipotizzato che si dovesse utilizzare un metodo con il quale selezionare i punti di misurazione con un metodo abbastanza semplice (…).  Tanto Nouwen quanto Greiner hanno notato che ogni dodecaedro ha i due fori più grandi esattamente uno di fronte all’altro. Greiner afferma anche che questi fori sono probabilmente fissati nella forma di cera. Questi fori di solito mostrano danni o irregolarità secondo Greiner. Se assumiamo che sia per questo motivo che i due fori non sono stati utilizzati come punti di misurazione, rimangono 10 aree per determinare una data, il che significa che ci sono un totale di 50 angoli misurabili. Con questi 50 punti di misurazione rimanenti, ho trovato il seguente sistema che è stato utilizzato con i dodecaedri. Dei restanti 50 punti di misurazione, solo 20 sono stati utilizzati per determinare una data. Funziona come segue:

1. Crea un’area orizzontale liscia su cui eseguire le misurazioni nel momento in cui il sole ha raggiunto il punto più alto della giornata.
2. Determina dove si trovano i due fori più grandi delle due aree opposte.
3. Poniti dietro l’area orizzontale in modo da guardare nella direzione del sole.
4. Posiziona il dodecaedro con uno dei due fori più grandi rivolto verso il basso e ruota il dodecaedro in modo tale che ci siano 5 aree inclinate in alto e puntate verso il sole e controlla se è presente una piccola macchia di luce.
5. Ora gira il dodecaedro senza sollevarlo, in modo da poter controllare le 4 aree rimanenti. Annota o ricorda quanti dei 5 punti di misurazione hanno attraversato la luce.
6. Posiziona il foro più grande verso il basso e ripeti le misurazioni. In totale, dovrebbero essere controllati 10 punti di misurazione.
7. Ora, posiziona il dodecaedro in modo tale che uno dei due fori più grandi si trovi sul lato inferiore sinistro (dal lato dell’utilizzatore) dell’area da cui dovrebbe passare la luce.
8. Controlla se è presente un piccolo punto luminoso, e ruota il dodecaedro attorno al suo asse immaginario che attraversa le due aperture più grandi e controlla i restanti 4 punti di misurazione. Le due aree con le aperture più grandi che sono opposte rimangono nello stesso posto con ogni punto di misurazione. In totale, avrebbero dovuto essere controllati 15 punti di misurazione.
9. Posiziona l’altra grande apertura nello stesso punto e ripeti la misurazione come descritto al n. 8. Tutti e venti i punti di misurazione devono essere controllati.

La misurazione sembra piuttosto difficile all’inizio, ma dopo un po’ di pratica può essere eseguita facilmente in 2 minuti  (…).

Esperimento personale

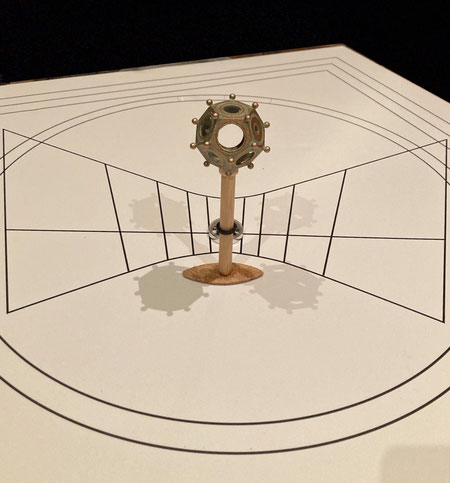
Al fine di poter verificare di persona l’attendibilità dello studio effettuato del Waemans, il sottoscritto ha acquistato da un costruttore spagnolo la riproduzione esatta del dodecaedro romano, conservato all’interno del castello di Saalburg, località dell’Assia, poco distante da Bad Homburg. Tale riproduzione è stata costruita usando una sofisticata stampante 3D, tanto da darne all’oggetto una precisione micrometrica. A confermare tale precisione il fatto che l’esemplare è dotato di tutte le piccole imperfezioni dovute al tempo, le scalfitture in uno dei due fori contrapposti di ugual diametro, dovute all’usura nell’inserire ripetutamente il dodecaedro nell’asta gnomonica per il suo sostegno, nonché l’usura delle palline, provocata dalle mani in coincidenza con l’asse di rotazione sull’asta gnomonica. Per completare i miei studi e prove sperimentali, non rimaneva che attendere il recente equinozio d’autunno, verificatosi il 22 settembre scorso. Aiutato anche dal filmato prodotto sempre dal Waemans (https://youtu.be/Hy8gVmL3xaA), e dopo essermi fatto fare anche un prototipo in  scala 1/1 della meridiana di Euporus, ho installato su una asta gnomonica dell’altezza di cm. 35,5 fissata nel punto in cui nell’originale ci sono ancora le tracce del foro, tramite un particolare dispositivo che mi garantiva la perfetta verticalità e complanarità, il dodecaedro romano.

Tutte le prove che ho svolto hanno dato un risultato sorprendentemente esatto per risalire al giorno coincidente con l’equinozio autunnale.

Conclusioni

Alla luce di queste ricerche e delle prove sperimentali condotte, anche personalmente, posso affermare con certezza che il dodecaedro romano venne impiegato dagli agrimensori romani nel periodo che va dal 230 a.C. fino al I secolo d.C., per individuare esattamente, alle varie latitudini, il giorno esatto dell’equinozio primaverile ed autunnale e quindi tracciarne perfettamente la sua retta equinoziale, punto di partenza per impostare con l’uso delle meridiane orizzontali, l’orientamento e la divisione/centuriazione delle terre conquistate, divenute colonie.

Luciano Cecconello

 

BIBLIOGRAFIA

Pubblicazioni ed articoli

P. ALBÈRI AUBER, La meridiana orizzontale di Aquileia – Il Plinto di Euporus. Gnomonica, Bollettino della Sezione Quadranti Solari, U.A.I. – n. 7, Trieste 2000.

P. ALBÈRI AUBER, “L’orologio solare orizzontale del Circo di Aquileia (2° sec. DC) il Plinto di Euporus, Prima Parte, Atti dell’Istituto Veneto di Scienze Lettere ed Arti, Tomo CLXIII (2004-2005) Classe di scienze Fisiche, matematiche e naturali. L’orologio solare orizzontale del circo di Aquileia –”Il Plinto di Euporus” Venezia 2005 .

P. ALBÈRI AUBER, “Antistius Euporus – nuovi aggiornamenti e ricerche su “Orologi Solari”, n. 11, Trieste 2016.

B.H. GREINER, “Dodecaeder, Tongern, Limburg” 1995

R. NOUWEN, “De Romeinse petagon-dodecaeder: mythe en enigma” 1993

Libri

A. PANTANALI, Le ore del sole. Meridiane del Friuli e della Venezia Giulia, Udine 2005.

A. ROVETTA, Cesare Cesariano. Vitruvio De architectura Liri II-IV. I materiali, i templi. gli ordini, Milano 2002.

C. CESARIANO De Architectrura di Marcus Vitruvius Pollio , Milano 1521.

D. J. PRINCE, de S. “Portable Sundials in Antiquity, including an Account ofa new Example from Aphrodisias”, Centaurus 14 (1969), 242-66.

G. PLINIUS, Plinio il Vecchio, Naturalis historia 77-78 d.C.

G. BRUSIN, Aquileia. Elementi della sua storia in Friuli. Luoghi e cose notevoli, Udine 1951.

G. BRUSIN, Aquileia e Grado. Guida storico-artistica, Padova 1956.

H. DIELS, Antiche Tecknik – Lipsia e Berlino 1920.

L BERTACCHI, Basilica, Museo e scavi – Aquileia, Roma 1994.

L. BERTACCHI, Nuova pianta archeologica di Aquileia, Udine 2003.

L. TITO, Ab Urbe condita (27 a.C. – 14 d.C.)  Liber XXi 63,

M. L. GATTI PERER, Cesare Cesariano e il Classicismo di primo Cinquecento. Atti del Seminario di studio (Varenna 7-9 ottobre 1994) Milano 1996.

E. N. LEGNAZZI, Del castro romano e di altri strumenti antichi di geodesia. Verona e Padova 1887

O. A. W. DILKE, Gli agrimensori di Roma antica, Bologna 1979.

P. KANDLER, Grado Aquileia, L’Istria 1865.

P. KANDLER, Indagini sullo stato materiale dell’Antica Aquileia, Trieste 1865.

P. KANDLER, Di Aquileia romana “in Archeografo Triestino” 1869.

P. KENNER, Sonnenuhren aus Aquileia, Kenner-Mittheilungen-K.u.K. Central Commission zur…-1880.

S. SETTIS (a cura di), Misurare la terra: centuriazioni e coloni nel mondo romano, Bologna 1984.

A. TAGLIAFERRI, Coloni e legionari nel Friuli celtico. Una ricerca archeologica per la storia, Pordenone 1986